这里的组合算法顾名思义,也就是组合,元素的组合。说到这里,可能会自然的联想到排列组合,但是排列组合生成的集合其实是组合算法的全集。很多时候我们面对的事物的排列组合比较少且简单,较为容易的就可以得出最佳组合。然而生活中也有一些很典型但是却不是那么容易发现以及直接解决的问题,就像我们接下来要谈到的三个问题,铺设线路,最短路径,选择地址。
接下来我将先讲解组合算法的贪婪策略,然后以问题为引导,分别说明三个问题中的贪婪策略,最后再拓展一下组合算法中的其他策略,或者说是其他思想。
贪婪策略
贪婪策略的核心是局部最优。这个策略是站着分冶法分解问题的基础上,假设我们子问题的最优解的总和就是原问题的最优解。如果问题真的是这种情况的话,这个问题又被称作拥有最优子结构。而使用贪婪策略的算法又叫做贪心算法。
贪心算法的特点是可行性,局部最优性和不可变更性。其中可行性是指算法的结果具有可行性。局部最优性是指对于问题的一部分来说是最优的,这是由贪婪策略决定的。不可变更性这个在与动态规划的对比中突出的比较明显,贪心算法和动态规划的区别就是在这里,贪心算法对于每个子问题的解决方案都做出决策,且不能回退;动态规划则会保留以前的运算结果,并根据以前的结果对当前进行选择,可以回退。
在算法中最常见的属于贪心算法的有Prim,Dijkstra,Kruskal。这三个都是求最小生成树的算法。
铺设线路(最小生成树)
题目
假设需要在油库 A 和加油站 B、C、D、E、F、G、H 之间修建输油管道,油库和各加油站的位置如图 10.6 所示,图中的虚线表示可能的管道铺设路线,虚线旁标注的数值表示所需铺设的管道的长度(千米)。例如油库 A 与加油站 B 之间需要铺 设 35 千米的管道。
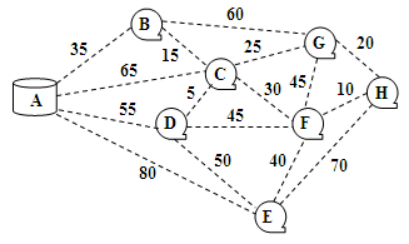
解题
为了简明快速的GET到题目的关键点,我们直观点来理解题目,我们要找到一个能够同时覆盖所有点的边的组合,使得总管道长最小。
题目的图可以直接对应一个加权图,然后我们直接运用最小生成图的算法就可以解决问题。这里最简单的算法应该说是Prim算法吧。
Prim算法的贪心策略在于层层递进,每一步都选取边权最小的边。
关于Prim算法和Kruskal算法,这里推荐一篇图文博文进行学习。
在通过Prim算法计算后,,我们大概可以得到这样的一个生成子图。
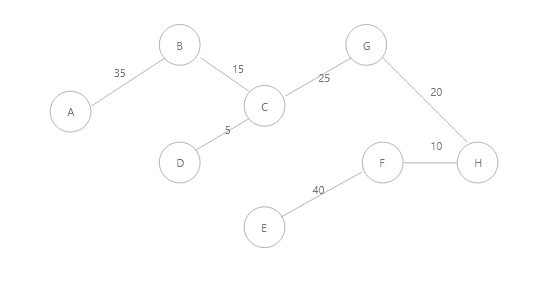
最短路径
题目
我们仍然采用上一题的图,提出四个问题
- 从A出发到其他点的最短路径。
- 以H为终点的所有最短路径。
- 从A到H的最短路径。
- 图中所有的最短路径。
解题
问题1、2、3
对于问题1、2、3,我们都可以直接使用Dijkstra算法计算。
问题4
对于问题4,可以使用Floyd算法解决。
拓展
这个题目中的四个题目分别对应着求最短路径的四类问题。
- 已知起点求最短路径。
- 已知终点求最短路径。在无向图中该问题与确定起点的问题完全等同,在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
- 已知起点和终点求最短路径。
- 求全局所有最短路径。使用Floyd-Warshall算法。
这当中还涉及到我们所求图的种类问题,很多算法对于图的种类是有要求的。更加详细的可以查阅资料,这里仅仅讨论解决问题。
选址问题
选址问题...作者表示现在暂时学不动,给出两个参考网站吧
总结与拓展
以上的内容,其实可以划分到运筹学的内容之中,运筹学是一门很博大的学科,但是很多专业只教授其中的一部分,如果有条件,应当系统学习一下。
本文只是超级粗略的说了给出了一些组合问题的解决措施,甚至没有具体的步骤,权当练手之作,希望读者原谅。
此外,本篇文章是以问题为导向,当中引用了一些解决问题的方法。如果读者感兴趣的话可以通过下面的知识列表进行拓展了解。
知识列表
- 离散数学--图论(图论的理论研究方向)
- 信息学--图论(图论的实际运用方向)
- 信息学--算法基础
- 运筹学--选址问题